5.1 Descriptive Statistics: Some popular Displays of Data
5.1.2 Organizing Quantitative Data
Tables
Original Data
| 2 | 2 | 2 | 4 | 5 | 3 | 3 | 3 | 3 |
| 2 | 1 | 2 | 3 | 5 | 3 | 4 | 3 | 1 |
| 2 | 3 | 5 | 3 | 2 | 1 | 3 | 2 |
Sometimes there are too many values to make a row for each one. In that case, we’ll need to group several values together.
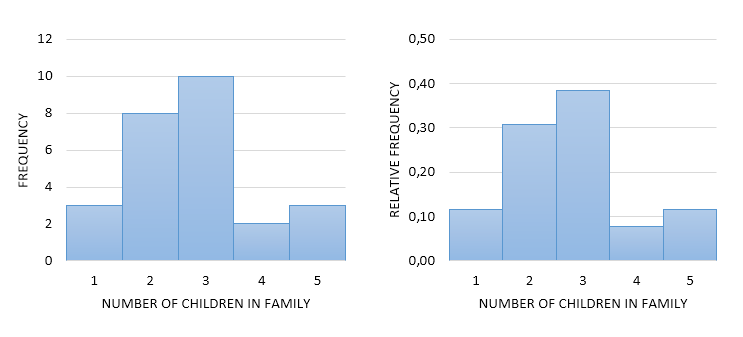
| children | frequency | Relative frequency | |
| 1 | 3 | 3/26≈ | 0.12 |
| 2 | 8 | 8/26≈ | 0.31 |
| 3 | 10 | 10/26≈ | 0.38 |
| 4 | 2 | 2/26≈ | 0.08 |
| 5 | 3 | 3/26≈ | 0.12 |
A discrete variable is a quantitative variable that has either a finite number of possible values or a countable number of values, i.e., 0, 1, 2, 3, …
Original Data
| 62 | 87 | 67 | 58 | 95 | 94 | 91 | 69 | 52 |
| 76 | 82 | 85 | 91 | 60 | 77 | 72 | 83 | 79 |
| 63 | 88 | 79 | 88 | 70 | 75 | 75 |
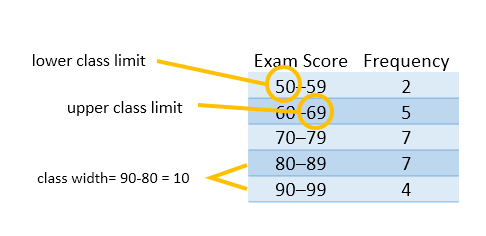
Histogram
| children | frequency | relative frequency |
|
| 1 | 3 | 3/26≈ | 0.12 |
| 2 | 8 | 8/26≈ | 0.31 |
| 3 | 10 | 10/26≈ | 0.38 |
| 4 | 2 | 2/26≈ | 0.08 |
| 5 | 3 | 3/26≈ | 0.12 |
Histogram
- height of rectangles is the frequency or relative frequency of the class
- widths of rectangles is the same and they touch each other
Frequency Polygon
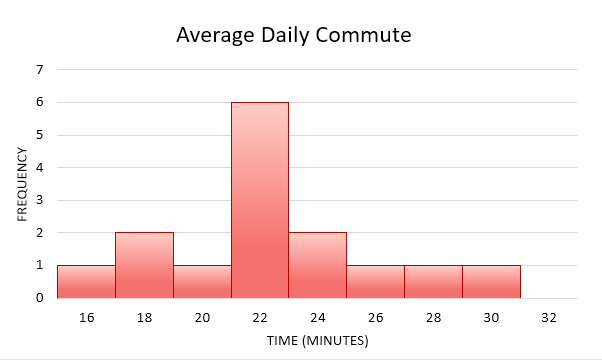
| average commute | frequency | relative frequency | |
| 16–17.9 | 1 | 1/15≈ | 0.07 |
| 18–19.9 | 2 | 2/15≈ | 0.13 |
| 20–21.9 | 1 | 1/15≈ | 0.07 |
| 22–23.9 | 6 | 6/15≈ | 0.40 |
| 24–25.9 | 2 | 2/15≈ | 0.13 |
| 26–27.9 | 1 | 1/15≈ | 0.07 |
| 28–29.9 | 1 | 1/15≈ | 0.07 |
| 30–31.9 | 1 | 1/15≈ | 0.07 |
A frequency polygon
is drawn by plotting a point above each class midpoint and connecting the points with a straight line.
(Class midpoints are found by average successive lower class limits.)
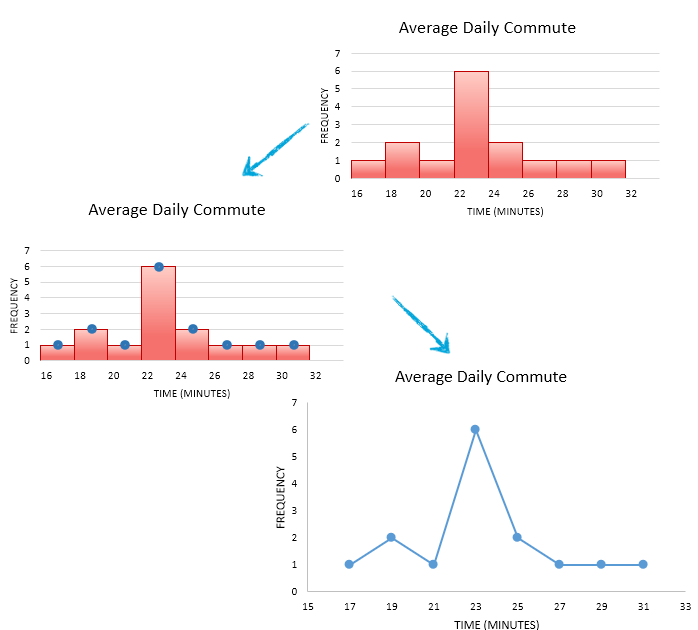
Cumulative Tables and Ogives
| average commute | frequency | cumulative frequency |
| 16–17.9 | 1 | 1 |
| 18–19.9 | 2 | 3 |
| 20–21.9 | 1 | 4 |
| 22–23.9 | 6 | 10 |
| 24–25.9 | 2 | 12 |
| 26–27.9 | 1 | 13 |
| 28–29.9 | 1 | 14 |
| 30–31.9 | 1 | 15 |
Cumulative tables
show the sum of values up to and including that particular category.
| average commute | relative frequency |
cumulative relative frequency |
||
| 16–17.9 | 1/15≈ | 0.07 | 1/15≈ | 0.07 |
| 18–19.9 | 2/15≈ | 0.13 | 2/15≈ | 0.20 |
| 20–21.9 | 1/15≈ | 0.07 | 1/15≈ | 0.27 |
| 22–23.9 | 6/15≈ | 0.40 | 6/15≈ | 0.67 |
| 24–25.9 | 2/15≈ | 0.13 | 2/15≈ | 0.80 |
| 26–27.9 | 1/15≈ | 0.07 | 1/15≈ | 0.87 |
| 28–29.9 | 1/15≈ | 0.07 | 1/15≈ | 0.94 |
| 30–31.9 | 1/15≈ | 0.07 | 1/15≈ | 1.00 |
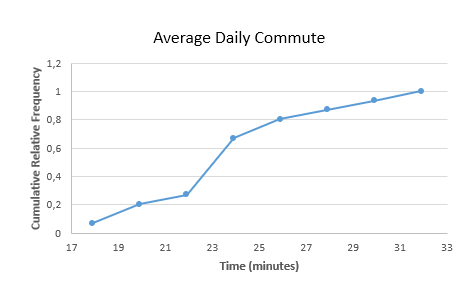
An ogive is a graph that represents the cumulative frequency or cumulative relative frequency for the class.
To the beginning of the section

