5.2 Inferential Statistics: Can the Results Be Generalized to Population?

5.2.2 Strength of a Relationship in Cross-Tabulation

 

Measures of Strength of Association between Variables

χ2 tests only the significance of an association and provides no statements about its strength.

Simple proof: doubling all values in the table doubles χ2.

Measures of the strength of association are:

• Phi Coefficient (φ)
• Contingency Coefficient (CC)
• Cramer’s V
• Lambda Coefficient (λ)

 

Phi Coefficient

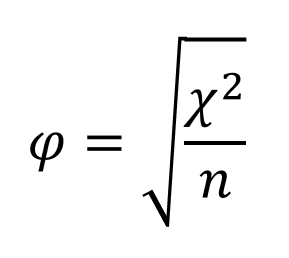
The higher φ, the stronger the association between the variables.

Values > .30 are considered substantial .

Problems:

• φ is not standardized, i.e., has a fixed upper limit of 1 only for 2×2 tables; depends on table’s dimensions.
• φ values from different studies cannot be compared.

 

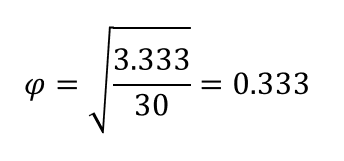
the association is not very strong

 

Contingency Coefficient

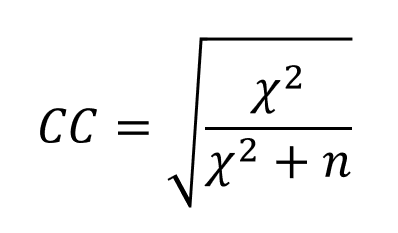
The higher CC, the stronger the association between the variables.

Values > .30 are considered substantial.

Although max. CC -value is limited by 1, it can be never achieved.

Problems:

• CC is not standardized, i.e., depends on table’s dimensions.
• CC values from different studies cannot be compared.

 

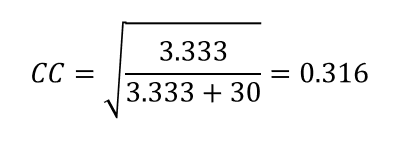
the association is not very strong

 

Cramer’s V

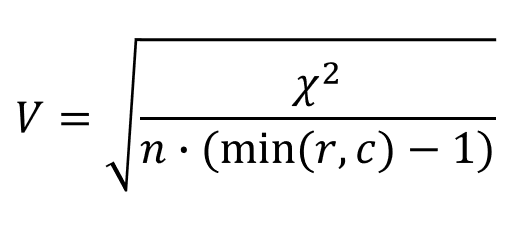
r – number of rows
c – number of columns

 

The higher V, the stronger the association between the variables.

Values > .30 are considered substantial.

maximum V -value is limited by 1, it can only be achieved in case of 2×2 tables.

Problems:

• V is not standardized, i.e., depends on table’s dimensions.
• V values from different studies cannot be compared.

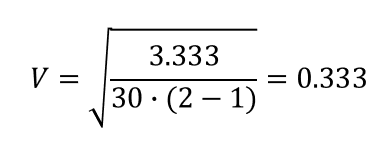
the association is not very strong

 

Lambda Coefficient

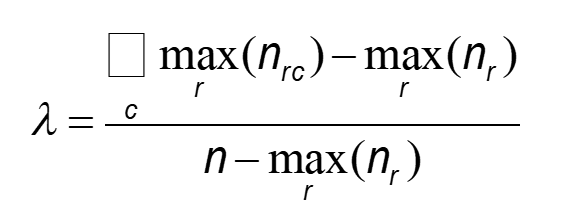
r – row index
c – column index

 

Measures the percentage improvement in predicting the value of the dependent variable, given the value of the independent variable.

Is standardized between 0 and 1 (1 indicates that the prediction can be made without error, 0 means no improvement in prediction).

Hence, λ-values can be compared among different studies.

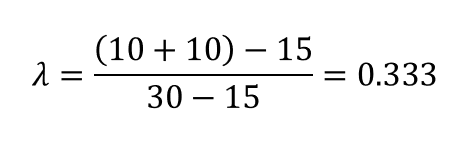
Knowledge of sex increases our predictive ability by the proportion of 0.333, i.e., a 33.3% improvement.

To the beginning of the section