4.Sampling
4.2 Probability Sampling
Require knowledge about the population
Simple Random Sampling & Systematic Sampling
Require knowledge about the population
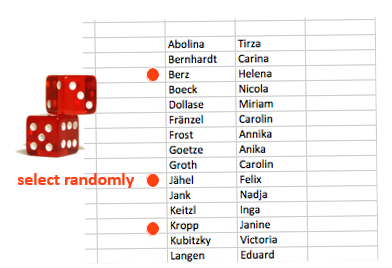
Simple Random Sampling
- Each element in the population has a known and equal probability of selection
- Each possible sample of a given size (n) has a known probability of being the sample actually selected
- This implies that every element is selected independently of every other element
Systematic Sampling
- The sample is chosen by selecting a random starting point and then picking every i-th element in succession from the sampling frame
- The sampling interval, i, is determined by dividing the population size N by the sample size n, i.e., i=N/n

Stratified Sampling
Require knowledge about the population
Stratified sampling is obtained by separating the population into non-overlapping groups called strata and then obtaining a proportional simple random sample from each group. The individuals within each group should be similar in some way.
Good for:
- highlighting a specific subgroup within the population
- observing existing relationships between two or more subgroups
- representative sampling of even the smallest and most inaccessible subgroups in the population
- a higher statistical precision
Proportionate
| Stratum | A | B | C |
| Population Size | 100 | 200 | 300 |
| Sampling Fraction | 1/2 | 1/2 | 1/2 |
| Final Sample Size | 50 | 100 | 150 |
Disproportionate
| Stratum | A | B | C |
| Population Size | 100 | 200 | 300 |
| Sampling Fraction | 1/5 | 1/2 | 1/3 |
| Final Sample Size | 20 | 100 | 100 |
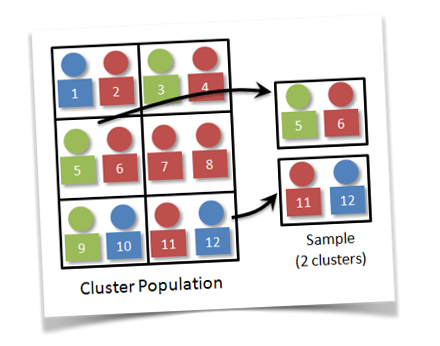
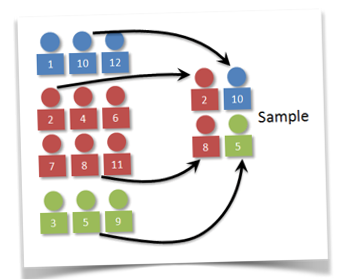
Cluster Sampling
Require knowledge about the population
Cluster sampling the target population is first divided into mutually exclusive and collectively exhaustive subpopulations, or clusters. Than a random sample of clusters is selected, based on SRS.
Good for:
- covering large geographic areas
- reducing survey costs
- when constructing a complete list of population elements is difficult
- when the population concentrated in natural clusters (e.g., blocks, cities, schools, hospitals, boxes, etc.)
For each cluster, either all the elements are included in the sample (one-stage) or a sample of elements is drawn probabilistically (two-sage).