4.Sampling
4.4 Sample Size
Determining the Sample Size
The sample size does not depend on the size of the population being studied, but rather it depends on qualitative factors of the research.
- desired precision of estimates
- knowledge of population parameters
- number of variables
- nature of the analysis
- importance of the decision
- incidence and completion rates
- resource constraints

Sample Sizes Used in Marketing Research Studies
| Type of Study | Minimum Size | Typical Size |
|
Problem identification research (e.g., market potential) |
500 |
1,000 – 2,000 |
|
Problem solving research (e.g., pricing) |
200 |
300 – 500 |
|
Product tests |
200 |
300 – 500 |
|
Test-market studies |
200 |
300 – 500 |
|
TV/Radio/Print advertising (per commercial ad tested) |
150 |
200 – 300 |
|
Test-market audits |
10 stores |
10 – 20 stores |
|
Focus groups |
6 groups |
10 – 15 groups |
Margin of Error Approach to Determining Sample Size
Margin of Error Approach to Determining Sample Size
The Margin of Error is the measure of accuracy of a survey. The smaller the margin of error, the more accurate are the estimates of a survey.
How accurate is this statistic? What is the margin of error?

Means
use this formula when evaluating estimates of population means
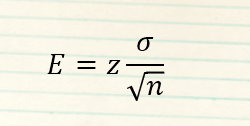
z = z-value for a given level of confidence
σ = standard deviation of a population parameter
n = sample size
Proportions
use this when evaluating estimates of proportions
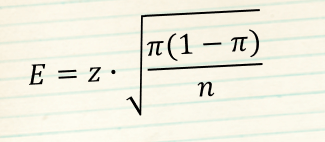
z = z-value for a given level of confidence
π = estimate of the proportion in the population
n = sample size


z-values
z = 1.96
for 95% level of confidence
z = 2.58
for 99% level of confidence
maximum margin of error for 95% level of confidence
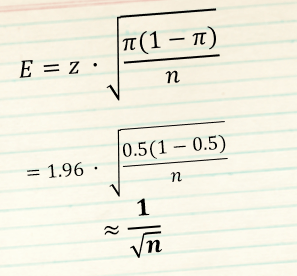
Margin of Error Approach to Determining Sample Size
How accurate is this statistic? What is the margin of error?
Margin of Error = 1/√n
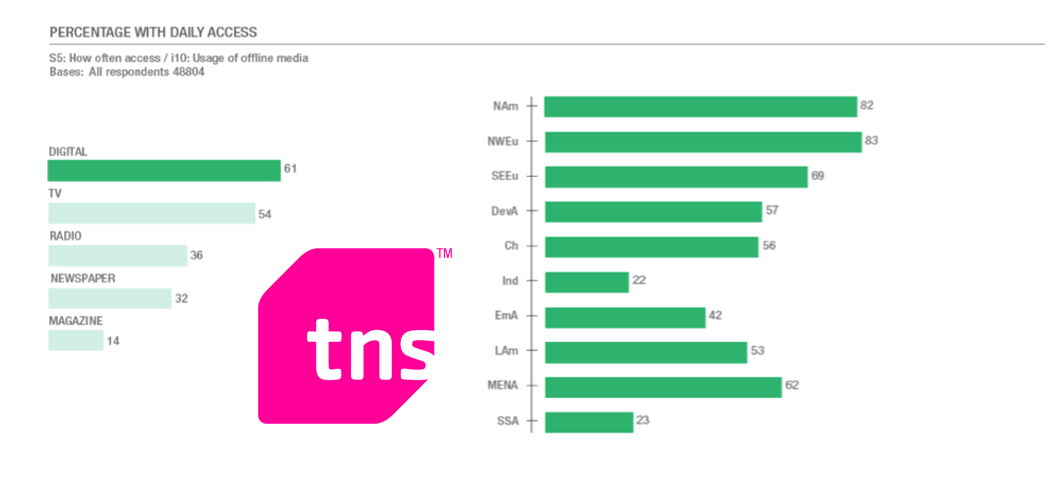
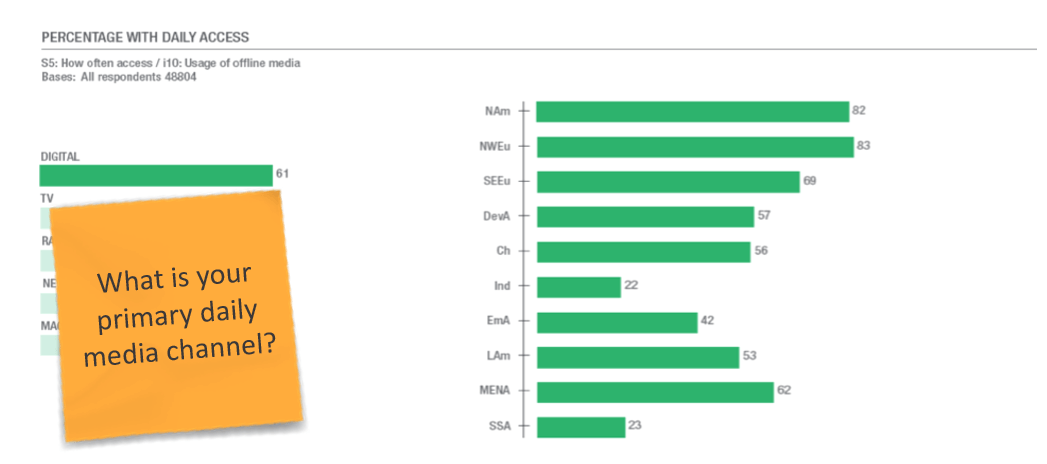
48,804 people in sample
√48,804=220.916
1/221 = 0.0045
*100 = 0.45%
⇒ x = 61% ± 0.45%
⇒ 60.55% to 61.45%
calculations are approximate values for 95% level of confidence
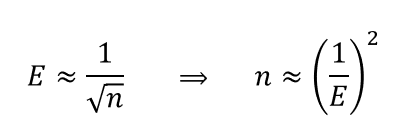
How large should the sample be taking margin of error of ±1% into account?
Sample Size = (1/Margin of Error)2
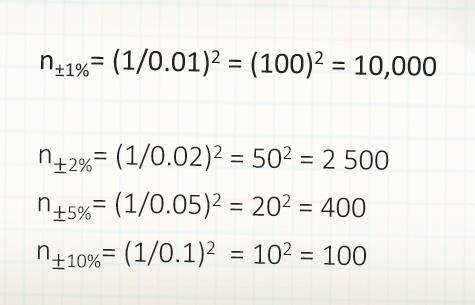
calculations are approximate values for 95% level of confidence
Corrections needed, when sample size exceeds 10% of the population
Sample Size = (1/Margin of Error)2
Sample Size does not depend on population.
n±1%= (1/0.01)2 = (100)2 = 10,000
What if the population under study consists of only 100 elements? (e.g., firms producing cars)
Correction of the Sample Size
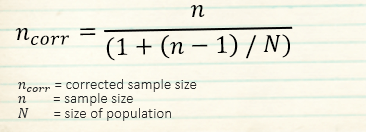
Margin of Error 1%
What if the population under study consists of only 100 elements? (e.g., firms producing cars)
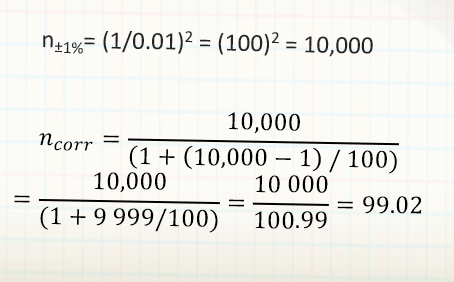
Margin of Error 5%
What if the population under study consists of only 100 elements? (e.g., firms producing cars)
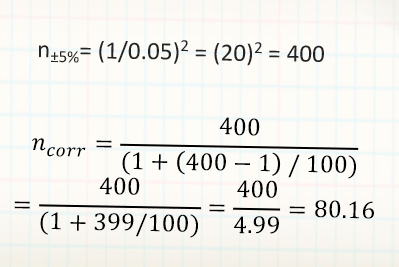
Margin of Error 10%
What if the population under study consists of only 100 elements? (e.g., firms producing cars)
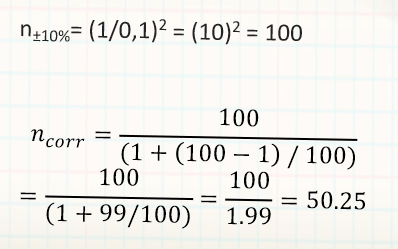
A Note on Confidence Interval
Confidence Interval & Level of Confidence
A confidence interval estimate is an interval of numbers, along with a measure of the likelihood that the interval contains the unknown parameter.
The level of confidence is the expected proportion of intervals that will contain the parameter if a large number of samples is maintained.
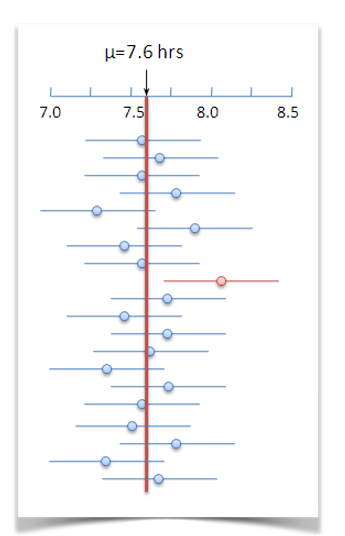
Suppose we’re wondering what the average number of hours that people at Siemens spend working. We might take a sample of 30 individuals and find a sample mean of 7.5 hours. If we say that we’re 95% confident that the real mean is somewhere between 7.2 and 7.8, we’re saying that if we were to repeat this with new samples, and gave a margin of ±0.3 hours every time, our interval would contain the actual mean 95% of the time.
Confidence Interval, Margin of Error, and Sample Size
The higher the confidence we need, the wider the confidence interval and the greater the margin of error will be
z-values
z = 1.96
for 95% level of confidence
z = 2.58
for 99% level of confidence
maximum margin of error for 99% level of confidence
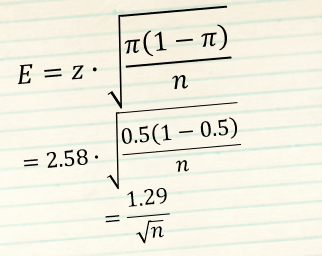
smaller margins of error
require larger samples
higher levels of confidence
require larger samples


